帮着同学打了一下北理的第一届新生赛，题目都十分有趣，收获满满。有一道是LLVM pass是容器题，就没打。
（当然，邪恶的代打行为被主办方正义制裁了，不过也是罪有应得啦）
大战WebAssembly#
给了一个 WebAssembly 的 check.wasm，外加一个 JavaScript 脚本逐字符验证 flag：
if (check(i, flag[i].charCodeAt(), enc[i]) != 1)逆向WebAssembly模块可知有check，f和g三个函数，总结下来一次check大概执行以下逻辑：
flag[i] = enc[i] XOR ((2*i + 1) XOR 8)写出解密脚本即可：
const enc = [
75, 66, 89, 124, 51, 64, 81, 65, 98, 76, 46, 46, 32, 76, 113, 39, 71,
24, 12, 112,
120, 19, 80, 0, 79, 8, 98, 10, 68, 80, 86, 4, 124, 126, 43, 58, 112,
114, 60, 24,
61, 104, 59, 108, 101, 100, 102, 51, 54, 92, 5, 92, 62, 91, 81, 87, 65,
79, 77,
78, 65, 29, 67, 40, 189, 229, 233, 208, 233, 178, 176, 216, 206, 175,
168, 242,
236,
];
let flag = [];
for (let i = 0; i < enc.length; i++) {
const v = enc[i] ^ ((2 * i + 1) ^ 8);
flag.push(String.fromCharCode(v));
}
console.log("FLAG =>", flag.join(""));什么？你问我怎么逆 WebAssembly 文件？IDA 9.2 直接打开就行啊，有 Loader 的。
答案：BITs2CTF{W311_d0n3!_Y0u'v3_5ucc355fu11y_d3f3473d_7h3_84084010n6_4nd_h15_W45m}
真假奶龙#
使用 Lua Decompiler 反编译Bytecode得：
-- filename: @./main.lua
-- version: lua54
-- line: [0, 0] id: 0
local function r0_0(r0_1)
-- line: [1, 20] id: 1
if type(r0_1) ~= "string" then
return "请输入文本"
end
r0_1 = string.reverse(r0_1)
local r1_1 = {}
for r5_1 = 1, #r0_1, 1 do
local r6_1 = string.byte(r0_1, r5_1)
if r6_1 >= 48 and r6_1 <= 57 then
table.insert(r1_1, (r6_1 + -48 + 2) % 9 + 48)
elseif r5_1 ~= 1 then
table.insert(r1_1, r6_1 + r1_1[r5_1 + -1])
else
table.insert(r1_1, r6_1)
end
end
return r1_1
end
local r1_0 = {
125,
158,
51,
84,
54,
171,
51,
146,
56,
134,
50,
51,
51,
54,
132,
227,
54,
149,
53,
167,
54,
149,
270,
51,
51,
54,
53,
167,
262,
379,
50,
171,
266,
48,
54,
158,
48,
143,
51,
164,
50,
54,
51,
139,
234,
50,
48,
143,
243,
53,
171,
50,
164,
276,
371,
53,
171,
210,
327,
50,
139,
234,
267,
53,
163,
50,
150,
245,
51,
51,
53,
140,
263,
333,
417,
484,
52,
167,
251,
324,
390
}
print("==========================")
print(" | 奶龙与小七之真假奶龙 | ")
print("==========================")
print("你：我是奶龙！")
print("假奶龙：我才是奶龙！")
print("你：我会喷火，你会吗？")
print("假奶龙：我也会！")
print("小七：你们别争了，真正的奶龙会念出只有我能听懂的神奇咒语！")
print("请输入你的咒语：")
local r3_0 = r0_0(io.read())
for r8_0 in pairs(r3_0) do
local r9_0 = r3_0[r8_0]
local r10_0 = r1_0[r8_0]
if r9_0 ~= r10_0 then
print("小七没有听懂你的咒语，你没有证明自己是真的奶龙！")
os.exit(1)
end
end
-- close: r4_0
print("恭喜你说出了正确的咒语，你是真的奶龙！")
os.exit(1)加密逻辑是典型的替换密码：
- 整体反转输入
- 从左到右扫描反转后的字符串：
- 如果是数字：用 (d+2) mod 9 的方式映射到另一个数字
- 如果是非数字 & 是第一个字符：直接用 ASCII 值
- 如果是非数字 & 不是第一个字符：把当前 ASCII 和前一个输出值相加
写出解密脚本：
r1_0 = [
125,158,51,84,54,171,51,146,56,134,50,51,51,54,132,227,
54,149,53,167,54,149,270,51,51,54,53,167,262,379,50,171,
266,48,54,158,48,143,51,164,50,54,51,139,234,50,48,143,
243,53,171,50,164,276,371,53,171,210,327,50,139,234,267,
53,163,50,150,245,51,51,53,140,263,333,417,484,52,167,
251,324,390
]
# 逆向数字分支：(c - 48 + 2) % 9 + 48
digit_map = {}
for d in range(48, 58): # '0'..'9'
enc = (d - 48 + 2) % 9 + 48
digit_map.setdefault(enc, []).append(d)
def reverse_enc(out):
"""
反推得到反转后的字符串（byte 数组）
"""
s_rev = [None] * len(out)
# i = 0，对应 Lua 的 i = 1
s_rev[0] = out[0] # 必须是非数字，直接就是 ASCII！
for i in range(1, len(out)):
val = out[i]
# 分支 1：尝试非数字分支：val = c + out[i-1]
c = val - out[i-1]
if 32 <= c <= 126 and not (48 <= c <= 57): # 可显示 & 非数字
s_rev[i] = c
continue
# 分支 2：尝试数字分支
if val in digit_map:
# 如果能对应到某些数字，那就是数字字符
# 多个可能时一般只有一个可打印
for d in digit_map[val]:
s_rev[i] = d
break
continue
raise ValueError("无法反推第 {} 项".format(i))
return s_rev
s_rev = reverse_enc(r1_0)
# 把 byte 数组拼成字符串，并反转回来
s = ''.join(chr(c) for c in s_rev[::-1])
print("解出的咒语：")
print(s)答案：BITs2CTF{W311_d0n3!_Y0u'v3_pr0v3d_70_X140q1_7h47_y0u_r3411y_4r3_4_N4110N6_1u4!1!}
ChaCha20#
简单到令人困惑的Python逆向，pycdc跑一遍就出来了
源代码：
# Source Generated with Decompyle++
# File: chacha20.pyc (Python 3.10)
from cryptography.hazmat.primitives.ciphers import Cipher, algorithms
from cryptography.hazmat.backends import default_backend
from Crypto.Util.number import long_to_bytes, bytes_to_long
from secret import flag
import time
import random
import os
def chacha20_encrypt(plaintext = None, key = None, nonce = None):
cipher = Cipher(algorithms.ChaCha20(key, nonce), None,
default_backend(), **('mode', 'backend'))
encryptor = cipher.encryptor()
ciphertext = encryptor.update(plaintext)
return ciphertext
if __name__ == '__main__':
k1 = bytes_to_long(os.urandom(32))
n1 = bytes_to_long(os.urandom(16))
print(f'''k1={k1}''')
print(f'''n1={n1}''')
random.seed(int(time.time()) % 100)
k2 = random.getrandbits(128)
n2 = random.getrandbits(64)
key = long_to_bytes(k1 ^ k2)
nonce = long_to_bytes(n1 ^ n2)
encrypted_data = chacha20_encrypt(flag, key, nonce)
print(f'''加密后: {encrypted_data.hex()}''')
return None解密脚本：
from cryptography.hazmat.primitives.ciphers import Cipher, algorithms
from cryptography.hazmat.backends import default_backend
from Crypto.Util.number import long_to_bytes
import random
# ================ 已知数据（从 result.txt 里抄过来的） ================
k1 =
89156737880809474145449532029493055444849328922741582677584755390029529653680
n1 = 20979402206073728478533457085044507592
ct_hex =
"a8c123f27ed9d34a6040a98f0b9d5e22930ca34bd3195e27a1e73725aba2f3eff888"
ciphertext = bytes.fromhex(ct_hex)
def chacha20_xor(data, key, nonce):
"""和原脚本一样，用 ChaCha20 做加解密（同一个操作）"""
cipher = Cipher(algorithms.ChaCha20(key, nonce), None, default_backend())
encryptor = cipher.encryptor()
return encryptor.update(data)
for seed in range(100):
random.seed(seed)
k2 = random.getrandbits(128)
n2 = random.getrandbits(64)
key = long_to_bytes(k1 ^ k2)
nonce = long_to_bytes(n1 ^ n2)
# 理论上 key 应该 32 字节，nonce 应该 16 字节，这里简单做个保护
if len(key) != 32 or len(nonce) != 16:
continue
try:
pt = chacha20_xor(ciphertext, key, nonce)
except Exception as e:
# 不符合要求长度等情况直接跳过
continue
# 简单筛一下：只要能 decode，且包含 CTF 常见格式就输出
try:
s = pt.decode("utf-8")
except UnicodeDecodeError:
continue
if "CTF{" in s or "BITs2CTF{" in s:
print(f"[+] seed = {seed}")
print(f"[+] plaintext = {s}")
break答案：BITs2CTF{pyc_reverse_is_important}
EasyMaze#
一眼的迷宫题。
查看代码发现没有做任何混淆，逻辑清晰易懂，代码可读性高，夸赞一下。
在 Maze::Maze 找到迷宫数据，排除反调试后的假数据，发现Maze类中除了前后左右外还有上下两个方向移动的函数，于是猜测应该是把三维迷宫逐层展开成一个二维迷宫（所以看起来是6*36的奇怪比例）。
相关代码截取发给AI后写出了美观的求解页面（非必须，个人喜好）
答案：BITs2CTF{QHGIIVVWRKECAEWNVUTQPHEEEGQ}
Gore#
Go语言逆向。
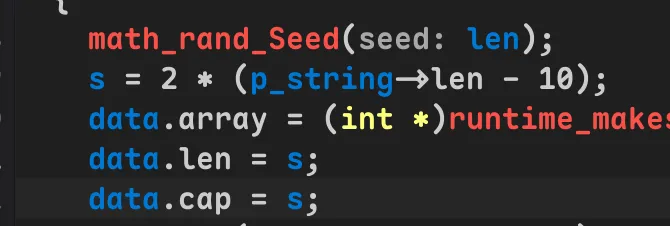这里是伪随机，但是Go版本未知，随机数生成逻辑可能和文档记录的不同。
查看 main_keyexpand 和 main_crypt 发现加密逻辑是环状XOR，但ran[]序列不方便完全静态复现。于是动调之：
pwndbg> info args
box = 0xc0001abea0
data = 0xc0001abed0
ran = 0xc0001abeb8
length = 56
pwndbg> x/gx (0xc0001abeb8)
0xc0001abeb8: 0x000000c0001bc1c0
pwndbg> x/56gx (0xc0001bc1c0)
0xc0001bc1c0: 0x0000000000000017 0x0000000000000068
0xc0001bc1d0: 0x0000000000000084 0x0000000000000017
0xc0001bc1e0: 0x0000000000000008 0x000000000000008f
0xc0001bc1f0: 0x00000000000000a6 0x00000000000000f2
0xc0001bc200: 0x00000000000000ea 0x000000000000002f
0xc0001bc210: 0x0000000000000053 0x00000000000000b1
0xc0001bc220: 0x00000000000000d3 0x00000000000000b6
0xc0001bc230: 0x00000000000000e2 0x000000000000005b
0xc0001bc240: 0x000000000000005c 0x000000000000009c
0xc0001bc250: 0x0000000000000058 0x0000000000000064
0xc0001bc260: 0x00000000000000f8 0x00000000000000a8
0xc0001bc270: 0x0000000000000022 0x00000000000000e2
0xc0001bc280: 0x0000000000000094 0x0000000000000005
0xc0001bc290: 0x0000000000000057 0x0000000000000069
0xc0001bc2a0: 0x0000000000000048 0x00000000000000fe
0xc0001bc2b0: 0x0000000000000020 0x0000000000000032
0xc0001bc2c0: 0x0000000000000078 0x00000000000000c1
0xc0001bc2d0: 0x0000000000000022 0x0000000000000053
0xc0001bc2e0: 0x00000000000000c9 0x0000000000000030
0xc0001bc2f0: 0x0000000000000047 0x00000000000000ac
0xc0001bc300: 0x000000000000001b 0x000000000000008f
0xc0001bc310: 0x000000000000003d 0x000000000000009f
0xc0001bc320: 0x0000000000000072 0x00000000000000df
0xc0001bc330: 0x00000000000000cd 0x0000000000000034
0xc0001bc340: 0x00000000000000ae 0x00000000000000fe
0xc0001bc350: 0x0000000000000032 0x00000000000000f9
0xc0001bc360: 0x00000000000000fc 0x000000000000005a
0xc0001bc370: 0x000000000000004e 0x0000000000000036写出解密脚本：
target = [
0xBE, 0x67, 0xF3, 0x76, 0xE1, 0x5C, 0xA0, 0x79,
0x1F, 0x42, 0xA7, 0x02, 0xE6, 0x99, 0x8D, 0xE3,
0xCE, 0x10, 0x30, 0x36, 0xF6, 0x1C, 0x1B, 0xA1,
0x4D, 0x25, 0x45, 0x43, 0xEE, 0x35, 0xFC, 0xB1,
0x87, 0xB3, 0xBB, 0x5D, 0x26, 0x1E, 0xE7, 0x08,
0x50, 0xFC, 0x4E, 0xA4, 0x7E, 0x45, 0xE6, 0xFC,
0xC9, 0x18, 0x38, 0x10, 0xA6, 0x4B, 0x7F, 0xD5,
]
ran = [
0x17, 0x68, 0x84, 0x17, 0x08, 0x8f, 0xa6, 0xf2,
0xea, 0x2f, 0x53, 0xb1, 0xd3, 0xb6, 0xe2, 0x5b,
0x5c, 0x9c, 0x58, 0x64, 0xf8, 0xa8, 0x22, 0xe2,
0x94, 0x05, 0x57, 0x69, 0x48, 0xfe, 0x20, 0x32,
0x78, 0xc1, 0x22, 0x53, 0xc9, 0x30, 0x47, 0xac,
0x1b, 0x8f, 0x3d, 0x9f, 0x72, 0xdf, 0xcd, 0x34,
0xae, 0xfe, 0x32, 0xf9, 0xfc, 0x5a, 0x4e, 0x36,
]
def keyexpand(k):
length = len(k)
box = list(range(256))
i = 0
j = 0
while i < 256:
v = box[i]
j_idx = (k[i % length] + v + j) % 256
box[i] = box[j_idx] ^ v
box[j_idx] ^= box[i]
box[i] ^= box[j_idx]
i += 1
j = j_idx
return box
def crypt(box0, data, ran):
length = len(data)
box = box0[:] # copy
i = 0
j = 0
t = 0
while t < length:
v7 = i - (((i + 1) & ~0xff))
idx_i = v7 + 1
v10 = box[idx_i]
j_idx = (v10 + j) % 256
box[idx_i] = box[j_idx] ^ v10
box[j_idx] ^= box[idx_i]
box[idx_i] ^= box[j_idx]
v16 = box[idx_i]
v17 = v7 + j_idx + 1
idx_ran = v17 % length
idx_s = ran[idx_ran] ^ ((box[j_idx] + v16) % 256)
data[t] ^= box[idx_s]
t += 1
i = idx_i
j = j_idx
return data
def invert_ring_xor(q):
L = len(q)
xor_0_to_Lm2 = 0
for i in range(L-1):
xor_0_to_Lm2 ^= q[i]
p0 = q[L-1] ^ xor_0_to_Lm2 ^ q[0]
p = [0]*L
p[0] = p0
acc = 0
for k in range(1, L):
acc ^= q[k-1]
p[k] = acc ^ p0
return p
def main():
key_str = "BITs2CTF{}"
k = [ord(c) for c in key_str]
box0 = keyexpand(k)
data = target.copy()
q = crypt(box0, data, ran.copy())
p = invert_ring_xor(q)
mid_bytes = []
for idx in range(28):
lo = chr(p[2*idx])
hi = chr(p[2*idx+1])
mid_bytes.append(int(hi+lo, 16))
middle = bytes(mid_bytes).decode()
flag = "BITs2CTF{" + middle + "}"
print(flag)
if __name__ == "__main__":
main()答案：BITs2CTF{G0r3_15_h@Aa4%&rD_7O_5oLv3?!}
Math#
fun1到fun4都是纯数学运算，可以化简成Z3求解器友好的形式。
from z3 import *
# 6 个 32-bit 无符号变量
A, b, c, d, e, f = BitVecs('A b c d e f', 32)
s = Solver()
# 范围约束：100000 < x < 1000000
lo = BitVecVal(100000, 32)
hi = BitVecVal(1000000, 32)
for v in (A, b, c, d, e, f):
s.add(UGT(v, lo)) # v > 100000
s.add(ULT(v, hi)) # v < 1000000
# 1) (A + b) % 951081 == 597141
mod = BitVecVal(951081, 32)
s.add(URem(A + b, mod) == BitVecVal(597141, 32))
# 2) A - b + 2c == 1644082
s.add(A - b + (c << 1) == BitVecVal(1644082, 32))
# 3) 4f XOR d == 1161537
s.add(((f << 2) ^ d) == BitVecVal(1161537, 32))
# 4) 5(d - e) == 343890
s.add((BitVecVal(5, 32) * (d - e)) == BitVecVal(343890, 32))
# 5) A + f == 1136538
s.add(A + f == BitVecVal(1136538, 32))
# 6) 2d + e == 1952901
s.add((d << 1) + e == BitVecVal(1952901, 32))
print(s.check())
m = s.model()
A_val = m[A].as_long()
b_val = m[b].as_long()
c_val = m[c].as_long()
d_val = m[d].as_long()
e_val = m[e].as_long()
f_val = m[f].as_long()
print("A =", A_val)
print("b =", b_val)
print("c =", c_val)
print("d =", d_val)
print("e =", e_val)
print("f =", f_val)
flag =
f"BITs2CTF{{{A_val:x}{b_val:x}{c_val:x}{d_val:x}{e_val:x}{f_val:x}}}"
print("Flag:", flag)答案：BITs2CTF{a5b51d446ddffa7a486593bbb6fc49}
这题本来想用Angr做符号执行，玩一把花活儿，结果Angr似乎跑进死循环了，可能还是学艺不精不太会用，sad😢😢。
Rustre#
Rust是一种很严谨的语言，所以当你尝试反编译rustre::main的时候你就会看到编译器摁造出来的依托垃圾。
各种边界检查丑的不要不要的，无法看出实际情况。于是让AI对代码进行简化（也就是说：写出一个等效Rust项目，这一步巨难无比，我花了一个下午才折腾出等效的可用代码）：
❯ cat src/main.rs
use std::io::{self};
// 对应 IDA 中的 rustre::square
// 在 Debug 编译下，Rust 会自动插入溢出检查 (is_mul_ok)
fn square(n: u32) -> u32 {
n * n
}
// 对应 IDA 中的 keychange
fn keychange(key: &mut [u8]) {
// 还原去重逻辑
// 遍历 1..4，比较 key[i] 和 key[i-1]
for i in 1..4 {
if key[i] == key[i - 1] {
key[i] = 50; // ASCII '2'
}
}
// 还原 XOR 链逻辑
// 遍历 0..3
for i in 0..3 {
key[i] ^= key[i + 1];
}
}
// 对应 IDA 中的 enc
// 这里包含了一个关键的逻辑陷阱，导致只加密了前 12 字节
fn enc(data: &mut [u8], key: &[u8]) {
let len = data.len();
// 陷阱还原：原作者可能想写 len / 4，但写成了 len / 8 (也就是 >> 3)
// 导致 limit = 28 / 8 = 3
let limit = len >> 3;
for i in 0..limit {
// 每次处理 4 字节
for j in 0..4 {
let data_idx = i * 4 + j;
// 密钥轮转逻辑: (Block + Offset) % 4
let key_idx = (i + j) % 4;
data[data_idx] ^= key[key_idx];
}
}
}
fn main() {
// 1. 读取输入
// 对应 std::io::stdio::Stdin::read_line
let mut input_str = String::new();
io::stdin()
.read_line(&mut input_str)
.expect("Failed to read line");
// 对应 core::str::trim
let input = input_str.trim();
// 对应 "Wrong length!" 检查
if input.len() != 28 {
println!("Wrong length!");
return;
}
let mut data = input.as_bytes().to_vec();
// 2. 准备密钥
let mut key_str = String::from("reee");
// SAFETY: "reee" is valid utf8, unsafe implies direct byte
manipulation in some contexts,
// but standard into_bytes is safe. kept simple here.
let mut key = key_str.into_bytes();
keychange(&mut key);
// 3. 执行加密 (含 Trap)
enc(&mut data, &key);
// 4. 位重组 (Shuffle)
// 对应那一长串的 index 操作。
// 使用 chunks(7) 会导致编译器对定长循环进行展开 (Loop Unrolling)
let mut shuffled_data = vec![0u8; 28];
for (chunk_idx, chunk) in data.chunks(7).enumerate() {
let base_idx = chunk_idx * 7;
// 模拟 7x7 位变换
for (s_byte_idx, &byte) in chunk.iter().enumerate() {
// 假设只处理 ASCII 的低 7 位
for b in 0..7 {
// 取出第 b 位
if (byte >> b) & 1 == 1 {
// 还原公式: dst = (6 - b - s) % 7
// 使用 rem_euclid 确保负数取模结果为正，符合数学定义
let d_byte_idx = (6 - (b as i32) - (s_byte_idx as i32)).rem_euclid(7)
as usize;
shuffled_data[base_idx + d_byte_idx] |= 1 << b;
}
}
}
}
// 5. 字节映射与比较
// 对应 IDA 中的 rustre::main::{{closure}}
// 以及最终的 cmp 逻辑
let target = [
139, 161, 68, 233, 197, 35, 129, 79, 171, 76, 167, 6, 37, 135, 207,
236, 143, 169, 41, 205,
8, 197, 109, 109, 205, 228, 140, 128,
];
// Map: ((x ^ 25) >> 3) | ((x ^ 25) << 5)
// 这在 Rust 中就是 rotate_right(3)
let final_data: Vec<u8> = shuffled_data
.iter()
.map(|&x| {
let val = x ^ (square(5) as u8);
val.rotate_right(3)
})
.collect();
// 6. 结果判定
if final_data == target {
println!("You are right!");
} else {
println!("You are wrong!");
}
}那还说什么，直接vibe it~
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
# 题目中 main 里给的 target 数组
TARGET = [
139, 161, 68, 233, 197, 35, 129, 79,
171, 76, 167, 6, 37, 135, 207, 236,
143, 169, 41, 205, 8, 197, 109, 109,
205, 228, 140, 128,
]
def keychange_from_reee():
"""
还原 Rust 里的 keychange("reee")
初始: "reee" -> [114, 101, 101, 101]
"""
key = [ord(c) for c in "reee"]
# 去重逻辑
for i in range(1, 4):
if key[i] == key[i - 1]:
key[i] = 50 # '2'
# XOR 链
for i in range(3):
key[i] ^= key[i + 1]
return key # [23, 87, 87, 101]
def inverse_map(target):
"""
逆向这一段：
val = x ^ 25
out = val.rotate_right(3)
对应逆过程：
val = rotate_left(x, 3)
src = val ^ 25
"""
res = []
for x in target:
# 8-bit rotate_left(3)
val = ((x << 3) & 0xFF) | (x >> 5)
res.append(val ^ 25)
return res # 得到 shuffled_data
def inverse_shuffle(shuffled):
"""
逆向 7x7 位重组：
正向：
for each chunk of 7 bytes:
for s in 0..6:
for b in 0..6:
if src[s] 第 b 位为 1:
d = (6 - b - s) mod 7
dst[d] 的第 b 位 |= 1
逆向：
已知 dst[d] 第 b 位为 1，则：
s = (6 - b - d) mod 7
src[s] 的第 b 位 |= 1
"""
n = len(shuffled)
out = [0] * n
assert n % 7 == 0
num_chunks = n // 7
for chunk_idx in range(num_chunks):
base = chunk_idx * 7
for d in range(7):
byte = shuffled[base + d]
for b in range(7): # 只处理低 7 位
if (byte >> b) & 1:
s = (6 - b - d) % 7
out[base + s] |= (1 << b)
return out # 即 enc 之后的 data
def inverse_enc(data_after_enc, key):
"""
逆向 enc：
正向：
limit = len >> 3 = 3 (因为 len=28)
i=0..2, j=0..3:
idx = i*4 + j
data[idx] ^= key[(i+j) % 4]
XOR 自反，所以逆向做同样的 XOR 即可还原。
"""
data = list(data_after_enc)
for i in range(3):
for j in range(4):
idx = i * 4 + j
kidx = (i + j) % 4
data[idx] ^= key[kidx]
return data
def main():
# 1. 逆最后一步 map，得到 shuffled_data
shuffled = inverse_map(TARGET)
# 2. 逆 7x7 位重组，得到 enc 之后但 shuffle 之前的 data
data_after_enc = inverse_shuffle(shuffled)
# 3. 还原 key
key = keychange_from_reee()
# 4. 逆 enc，得到原始输入（flag 字节）
plain_bytes = inverse_enc(data_after_enc, key)
# 5. 转成字符串
flag = ''.join(chr(b) for b in plain_bytes)
print("Recovered flag:", flag)
if __name__ == "__main__":
main()答案：BITs2CTF{D1fficuLt_Ru57R3~~}
这个题目还是很有难度的，1kpts名副其实。传统的长代码审计也很克制 AI 。我使用Gemini3分步处理，非常完美的解决了这道题目，令人感叹长上下文就是爽啊~
另外值得提一嘴的就是AI的使用。这些日子大量使用AI辅助做题，发现了一个小技巧：我们把AI的解题步骤分为提供信息和思路推进，则思路推进一定要分步处理，信息提供一定要一步给完
如何理解这句话呢？例如有fun1()、fun2()两个函数，经过了3个不同的加密步骤得到密文。
则，你的第一条prompt应该是：fun1()的完整代码+fun2()的完整代码+调度器（让AI知道是3轮加密），2️而不应该是：第一条prompt给fun1()的代码，AI提示你给出fun2()的，你再给。
一次给足信息的效果几乎总是远远强于分步给出信息的会话，fun fact to share.
感想#
最近很不顺心，打N1打的有点破防，结果看到这篇博客 ↗，震惊地发现：设计这道卡住我一周的难题的，位列N1官网的师傅，竟然才大二（或大三）。一瞬间被差距打击地体无完肤了，迫切地想做题做题做题。
这种心态健康吗？也不见得多健康，熬夜，眼睛痛，头晕，上课打不起精神，作业欠一堆，还有那些自己处于体验生活目的加入的学生社团和组织的任务…算了，你没有义务成为天才，还是过好自己的生活吧。
You only live once.